Before looking at the details of asset class investing, we first need to learn about investment risk—what it means, and how to manage it.

Perhaps the single most important lesson in all of investing is that risk and return are always related. If you seek safety, you will receive a low return. If you seek a higher return, you must take on risk.

What do we mean by risk? We mean the potential to lose money. How do we characterize an asset class’s potential for losing money? By its volatility.

If an asset class like Brazilian stocks grows 50% this year, but loses 45% next year, then it has a high volatility—it’s risky. If an asset class like government bonds returns 1.5% this year, and 1.6% next year, it has low volatility—it’s not so risky.

Let’s look at the range of returns of various asset classes during the 20-year period from 1991 to 2010, as well as their annualized returns over that same period.

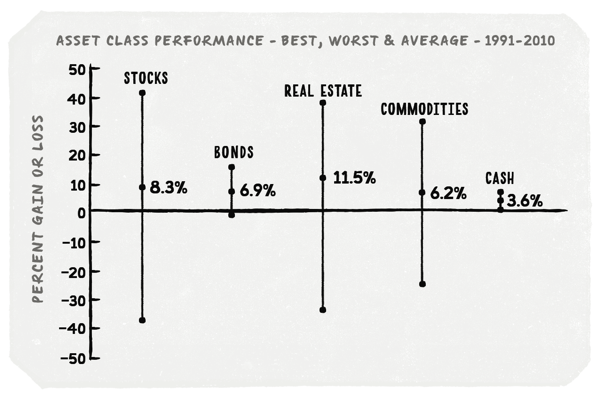
Intuitively, we can see that stocks, real estate and commodities are riskier than bonds and cash. In their best year, stocks returned over 40%, but in their worst, they lost nearly 40%. But over the whole 20 years, stocks had an annualized return—which you can think of as a kind of average—of about 8%.

Invested in cash, we wouldn’t have lost money in any particular year, but we would have only earned an annualized return of about 3.5% over the 20 years. And we’ve seen the huge difference in compounding effect an additional 4.5% can make!

The volatility of an asset class is expressed by a statistical measure called standard deviation. We won’t focus on the mathematical meaning of that in this book—just remember it’s a measure of risk.

In this book, we’ll be recommending to take on risk in the form of investing in volatile asset classes like stocks. We’ll also learn ways of mitigating the effects of taking on that risk.